
#NONLINEAR REGRESSION EXCEL SERIES#
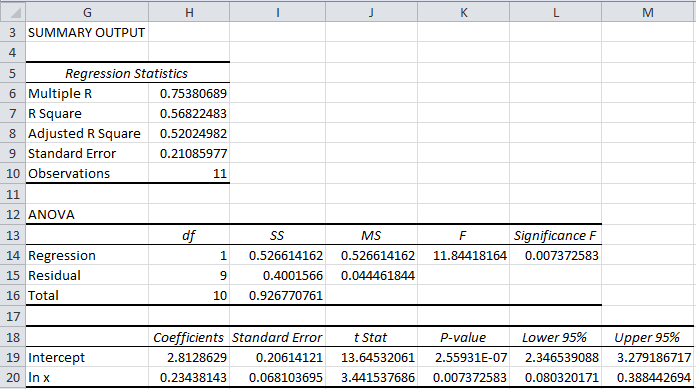
In other words, splines are series of polynomial segments strung together, joining at knots (P. Polynomial regression is computed between knots. Splines provide a way to smoothly interpolate between fixed points, called knots. An alternative, and often superior, approach to modeling nonlinear relationships is to use splines (P. Polynomial regression only captures a certain amount of curvature in a nonlinear relationship. Stat_smooth(method = lm, formula = y ~ poly(x, 5, raw = TRUE)) Visualize the fith polynomial regression line as follow: ggplot(train.data, aes(lstat, medv) ) + RMSE = RMSE(predictions, test.data$medv), # lm(formula = medv ~ poly(lstat, 6, raw = TRUE), data = train.data) The following example computes a sixfth-order polynomial fit: lm(medv ~ poly(lstat, 6, raw = TRUE), data = train.data) %>% The output contains two coefficients associated with lstat : one for the linear term (lstat^1) and one for the quadratic term (lstat^2). # (Intercept) poly(lstat, 2, raw = TRUE)1 # lm(formula = medv ~ poly(lstat, 2, raw = TRUE), data = train.data) The polynomial regression can be computed in R as follow: lm(medv ~ lstat + I(lstat^2), data = train.data)Īn alternative simple solution is to use this: lm(medv ~ poly(lstat, 2, raw = TRUE), data = train.data) # In R, to create a predictor x^2 you should use the function I(), as follow: I(x^2). The polynomial regression adds polynomial or quadratic terms to the regression equation as follow: The best model is the model with the lowest RMSE and the highest R2. The R2 represents the squared correlation between the observed and predicted outcome values. Recall that, the RMSE represents the model prediction error, that is the average difference the observed outcome values and the predicted outcome values. The RMSE and the R2 metrics, will be used to compare the different models (see Chapter regression)).
#NONLINEAR REGRESSION EXCEL HOW TO#
In this chapter, you’ll learn how to compute non-linear regression models and how to compare the different models in order to choose the one that fits the best your data. Fits spline models with automated selection of knots. The values delimiting the spline segments are called Knots. Fits a smooth curve with a series of polynomial segments. It add polynomial terms or quadratic terms (square, cubes, etc) to a regression. This is the simple approach to model non-linear relationships.
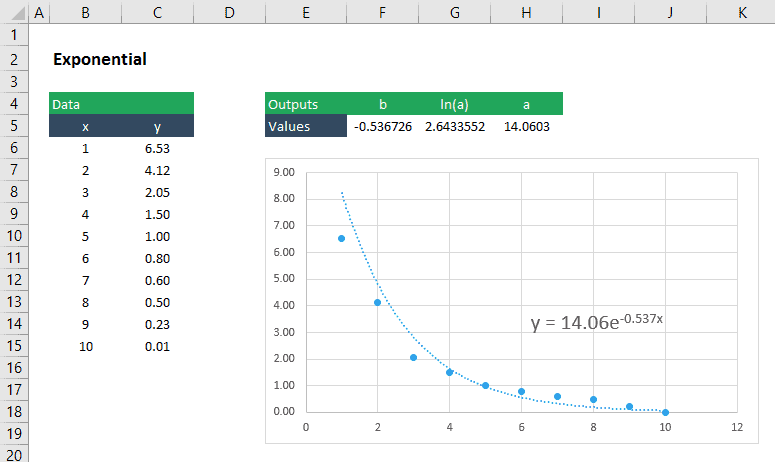
There are different solutions extending the linear regression model (Chapter for capturing these nonlinear effects, including: In some cases, the true relationship between the outcome and a predictor variable might not be linear.


 0 kommentar(er)
0 kommentar(er)
